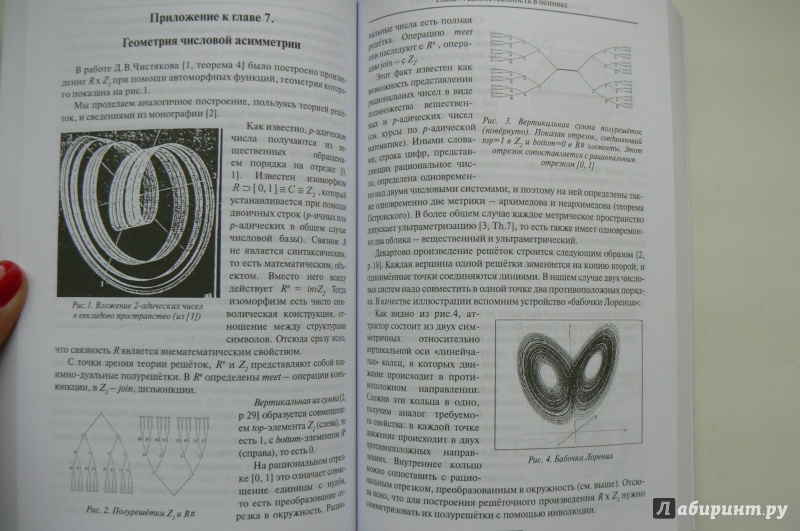
Все, что вам нужно знать о кольце в математике: основные понятия и правила

Кольцо в математике - это алгебраическая структура, включающая в себя две операции и набор аксиом. Оно является основой для изучения таких важных областей, как алгебра, теория чисел и анализ.

При изучении кольца в математике, важно понять его определение и основные свойства.

Изучайте примеры конкретных кольцов, чтобы лучше понять их структуру и применение.

Не забывайте о коммутативности операции умножения: в коммутативных кольцах она выполняется, в некоммутативных - нет.

Обратите внимание на наличие нулевого и единичного элементов в кольце: они играют важную роль во многих доказательствах и рассуждениях.

Изучайте свойства и условия, при которых элемент кольца обратим, а также свойства делителей нуля.

Применяйте знания о кольцах в других областях математики, таких как геометрия, криптография и теория кодирования.

Углубляйтесь в изучение различных типов колец, таких как целочисленные кольца, многочлены и дробные числа, чтобы расширить свои знания в математике.

Используйте кольца в решении задач и проблем различных областей науки и техники, таких как физика, экономика и компьютерные науки.

Общайтесь с другими студентами и математиками, чтобы обсудить и разделить свои знания о кольцах и их применении.

Не бойтесь задавать вопросы и искать дополнительную информацию о кольцах - это поможет вам лучше понять математику и ее приложения.